Natural numbers form a component of the system of numbers that includes all positive numbers that range from 0 to infinite. Natural numbers are also referred to as counting numbers because they don’t contain zero numbers or negative ones. They form elements of the real number, comprising only positive integers; however, they do not include decimals, fractions, zeros and negative numbers. We will discuss the nature of natural numbers and the natural numbers in this article.
Natural Number Definition
In the introduction section, Natural numbers are numbers that are positive integers and include numbers from one to infinite(). They are countable and generally utilized for calculation purposes. The natural number set is symbolized by the alphabet “N”.

N =1,2,3,4,5,6,7,8,9,……………….
Modern definitions
In 19th-century Europe, There was a philosophical and mathematical discussion concerning the precise nature of natural numbers. Henri Poincare stated that hypotheses cannot be proven through their limited application, concluding that it’s “the ability to think” that allows us to imagine an indefinite repetition of the same action. 19 Leopold Kronecker summarized his belief in the following way: “God created the integers, and all other work is the responsibility of humankind”. [g]
The constructivists believed that there was a necessity for improvement of the logical rigour of the mathematical foundations. In the early 1860s, Hermann Grassmann suggested a”recursive” definition for natural numbers. This meant that they were not natural but as a result of definitions. In the following years, two types of formal definitions were developed, and later, the two classes were found to have the same meaning in a majority of instances.
Natural numbers that are set-theoretical originated with Frege. He first defined a “natural” number as the category of every set within one-to-one correspondence to the set in question. But, his definition was a source of contradictions, such as Russell’s paradox. To avoid these paradoxes, the definition was changed in such a way that a natural quantity can be defined as a distinct set, and any other set which can be placed in one-to-one correspondence to that set is said to possess this amount of elements. [22]
The second category of definitions was conceived in the work of Charles Sanders Peirce. It was developed by Richard Dedekind and further investigated by Giuseppe Peano; this approach has been dubbed Peano mathematical. The basis of the concept is the axiomatization of ordinal numbers: every natural number is a successor, and each natural number that is non-zero has a unique predecessor. Peano’s arithmetic is compatible with a variety of weak sets of set theory. One of them is ZFC, which has the hypothesis of infinite replaced by its negative. Theorems which ZFC can demonstrate, however, cannot be proven with Peano Axioms. Peano Axioms include Goodstein’s theorem. [23]
Set of Natural Numbers
In math, the natural set of numbers can be expressed in terms of 1,2, 3, … The natural numbers are depicted as an N symbol. N is. An assortment of elements is known as a “set” (numbers in this case). The smallest element of N is one, and the following element can be described by the number 1. N is any element within N. 2 is higher than 1, 3 is greater than two, and the list goes on. This table will explain the various set types of natural numbers.
Natural numbers form the subset of total numbers. Whole numbers constitute the subset of the integers. In the same way, integers constitute the real number subset. This diagram will explain the connection w.r.t. the different sets of natural numbers as well as whole numbers, integers and real numbers.
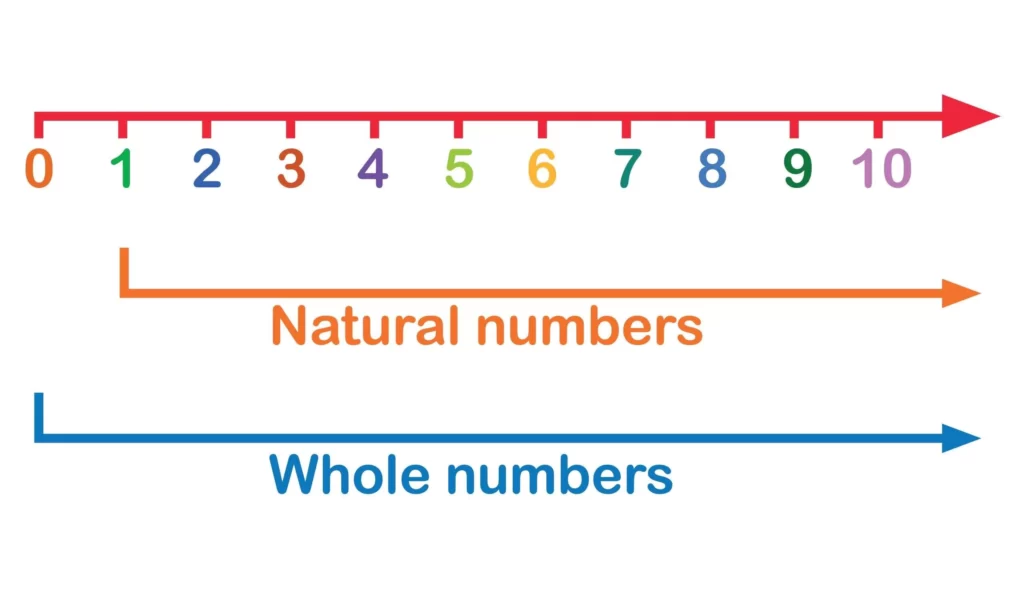
Natural Numbers and Whole Numbers on the Number Line
number line
We have already discussed that all positive integers are natural numbers. Hence, on the line of numbers, those numbers to the right from the zero (0) mark are all natural numbers. Positive integers that include zero are considered to be whole numbers.
History of Natural Numbers
It is thought that natural numbers came from words for counting objects. They start with one. A place value scheme for numbers one (one) as well as 10 (ten) was initially developed by Babylonians.




